[DLBasic] 9-2. BackPropagation

     저번 시간에 이어서 W1, W2, b1, b2를 어떻게 설정하는 것이 좋을지 알아보도록 하겠다.

 

     우리가 최종적으로 구하고 싶은 것은 cost function이 최소가 되는 weight과 bias이다. cost function의 최소값을 구하려면 이전에도 사용했었던 gradient descent를 사용해야하고, 이 때 미분을 사용한다.

 

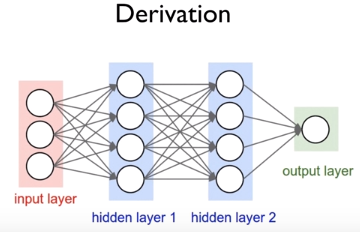
     그런데 Neural Network에 이 미분을 적용하려면 노드의 개수도 많아지고 중간에 sigmoid 함수 등을 사용하기 때문에 input, 중간 값들이이 output값에 미치는 영향을 알기가 힘들고 계산하기도 힘들다는 문제가 있었다.

 

     이전에도 설명했듯이 Back Propagation을 이용해서 뒤에서부터 에러를 전달해서 앞에서 어떻게 weight과 bias를 설정할지 정할 수 있다.

 

Back Propagation using Chain Rule

Chain Rule

        미분을 할 때 chain rule을 사용한다. x로 f를 미분한 식을 바로 알아내기 힘들 때 먼저 g로 f를 미분하고 그 결과에 x로 g를 미분한 결과를 곱해서 결과적으로 알아내는 것이다.

Forward

      처음의 forward는 위와 같이 간단하게 w와 x를 곱하고 b를 더하는 형식으로 이루어진다.

 

Chain Rule을 사용한 Back Propagation

     이제는 backpropagation을 하기 위해서 먼저 기본적으로 사용되는 미분을 미리 해놓을 것이다.

x로 g를, w로 g를, g로 f를, b로 f를 미리 미분해놓는다. 그 이후에는 f를 w로, f를 x로, b로 f를 미분하는 것이 chain rule을 통해서 쉽게 할 수 있다. f를 w,x,b로 미분한 결과는 f의 값을 좌우한다. 만약 b로 f를 미분한 값이 1 증가한다면

f의 값도 1이 증가하여 -6이 될 것이다.

     실제로는 위와 같이 많은 단계가 있을 수 있다. 이 많은 단계를 해결하기 위해서는 당황하지 말고 하나씩 미분을 해서 해결해나가면 된다. 즉, a와 b로 f를 미분한 값을 먼저 구하고 그것을 이용해 계속 앞으로 나아가서 결국 처음의 입력까지 다다르는 것이다.

     그렇게 입력값 바로 앞까지 다다라서 g로 f를 미분한 값이 도착하면 일단 x로 g를 미분한 결과는 

알 수 있다. 왜냐하면 g = x * y인 것을 이미 알기 때문이다.

시그모이드의 미분을 backpropagation으로

     이것을 이용해서 시그모이드의 미분을 한 번 생각해보자. 맨 뒤로부터 앞으로 각각 미분값을 구한 다음에 곱하면서 나아가면 아무리 어려운 식이더라도 쉽게 결과를 구할 수 있다고 한다.

tensorflow에서 backpropagation의 사용

      tensorflow에서 backpropagation은 위와 같이 이미 구현되어있어서 쉽게 사용할 수 있다.