이번 시간에는 balanced search tree 중 하나인 red-black tree에 대해 알아보도록 하겠다.
● Red-Black Tree
- red-black tree는 binary search tree로써, 아래의 4가지 조건을 만족한다.
① Root Property : root는 검은색이다.
② External Property : 모든 leaf node들은 검은색이다.
③ Internal Property : 빨간 노드의 자식들은 검은 노드이다. (부모와 자식이 모두 빨간색인 경우는 없다.)
④ Depth Property : 모든 leaf node들은 같은 black depth를 가져야한다.
* black depth
- 어떤 노드에서 root까지 가는 경로에 있는 black 노드들의 수.
- 보통 leaf에서 시작해야 의미가 있고, red-black tree에서는 어떤 leaf node에서 시작하던지 root까지 가는 경로에서
만나는 black 노드들의 수는 같다.

● Height of a Red-Black Tree
- n개의 노드들이 있는 red-black tree에서의 높이는 O(logn)이다.
→ 정확히 왼쪽, 오른쪽으로 개수가 n/2씩으로 반반 나뉘어지지는 않지만, balanced이므로 O(logn)로 bound된다는
사실만 알자. 가장 depth가 큰 경우와 가장 depth가 작은 경우는 맨 아래에서 증명했듯이 기껏해야 2배 정도만
차이난다.
- red-black tree에서의 탐색 알고리즘은 binary search tree에서의 탐색 알고리즘과 같고, O(logn) 시간이 걸린다.
* red-black tree에서의 depth의 최대 차이
- external node의 최대값이 그 tree의 높이이다.
- black depth가 x라고 했을 때, depth가 최소인 경우는 black만 계속 있는 경우로 depth는 x겠고,
depth가 최대인 경우는 black-red-black-red-... 이런 식으로 black, red가 교차되어 나열되어있는 경우로 depth는
2x에 해당할 것이다.
- 이렇게 가장 깊은 경우와 가장 얕은 경우가 기껏해야 2배 차이이므로 꽤나 balanced된 tree라고 할 수 있다.
● Insertion
- 편의상 key들이 중복된 것이 없는 unique한 상태라고 하자.
- insertItem(k, o)는 key가 k인 노드 o를 삽입한다는 것이고, 이를 수행하려면 새롭게 삽입되는 노드 z를 무조건 빨간색으로 해야한다.
- 기존의 binary search tree에서의 insert와 마찬가지로 다음의 단계로 insert한다.
① key가 k인 object가 tree에 이미 있는지 search한다.
→ 어차피 맨 처음 조건에 key는 중복되지 않는다고 했으니 어차피 없긴 할 것이다.
→ leaf까지 가야 해당 key가 이미 있는지 없는지 알 수 있을 것이다.
② 없다는 것을 확정한 그 자리에 internal node를 만들고 원래 있었던 leaf 노드들을 똑같이 매달아준다.
- 그러면 맨 처음에 red-black tree의 네 조건들 중 root, external, depth의 세 속성들은 만족한다.
- 만약 삽입하는 노드 z의 부모인 v가 black인 경우는 internal property까지 만족하므로 끝난다.
- 하지만 만약 v가 red라면 internal property를 위반하므로 tree의 reorganization이 필요할 것이다.
- 새로 삽입된 node가 red이기 때문에 삽입 전과 후에 black depth는 일정하게 유지된다.
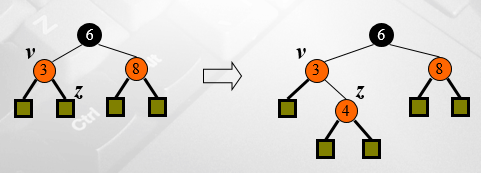
- 이제 parent가 red인 경우에 어떻게 reorganization을 하는지 알아보도록 하자.
● Remedying a Double Red
- 부모와 자식이 동시에 red인 경우는 internal property를 위반한 것이고, 그것을 바로잡는 것은 두 가지 경우로
나뉘어진다.
-아래와 같이 부모 v의 형제(z의 입장에서는 uncle node)인 w가 black인 경우는 restructuring을 한다.

- 아래와 같이 uncle node가 red인 경우는 recoloring을 한다.

① Restructuring
- 아래 그림과 같이 원래 root를 left subtree로, v는 그대로, 삽입된 노드 z를 root로 하고 색을 black으로 바꿔준다.
- 그림에서는 나와있지 않지만 원래 있었던 subtree들이 T0, T1, T2 순으로 그대로 달릴 것이다.


- 위의 그림에서 왼쪽 두 경우는 double rotation, 오른쪽 두 경우는 single rotation을 거치고, 결과는 모두 같다.
- 그림에서는 나와있지 않지만 원래 있었던 subtree들이 T0, T1, T2, T3 순으로 그대로 달릴 것이다.
- 총 O(1) 시간이 걸리고 복잡하긴 하지만 느리진 않는다.
② Recoloring

- 부모인 v와 그 형제인 w를 둘 다 black으로 만들어주고, 그들의 부모(새로 삽입된 노드 z의 입장에서는 grandparent)의
색을 red로 바꿔준다.
- 이러면 grandparent의 parent가 red였을 경우 double red 현상이 또 일어날 수도 있다.
→ root까지 올라가면서 똑같이 고쳐주자.
- uncle, parent 모두 black으로 바꾸는 것은 O(1) time, 그 윗부분 재구성하는 것은 추가의 시간이 걸릴 것이고, 모든
노드의 black depth가 1씩 증가할 것이다.
- restructuring, recoloring 모두 black depth는 일정할 것이다.
다음 시간에는 그래프에 대해 배우도록 하겠다.
'CS > Algorithm' 카테고리의 다른 글
| [Algorithm] 6-2. Binary Search Tree (0) | 2020.04.28 |
|---|---|
| [Algorithm] 7-1. Graphs and Graph Traversals (0) | 2020.04.28 |
| [Algorithm] 2. Data Abstraction and Basic Data Structures (0) | 2020.04.26 |
| [Algorithm] 1-2. Mathematical Background (0) | 2020.04.26 |
| [Algorithm] 1-1. Analyzing Algorithms and Problems - Introduction (0) | 2020.04.26 |


