알고리즘 문제를 해결해나가면서 알면 문제를 더 빠르고 쉽고 정확하게 풀 수 있는 알고리즘을 정리해보겠다.
● 제곱근 구하기 → 바빌로니아 법
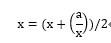
a는 제곱근을 원하고자 입력되는 값이고, x는 0~a 사이에 존재하는 임의의 값이다.
이 수식을 원하는 근사치가 나올 때까지 반복 루프를 돌린다.
루프를 많이 돌릴수록 제곱근의 정확도가 높아진다.
● 소수인지 판별하는 알고리즘 → 에라토스테네스의 체 (Sieve of Eratosthenes)
#include <cmath>
bool isPrime(int a) {
if (a == 1)
return false;
else {
int end = sqrt(a);
for (int j = 2; j <= end; j++) {
if (a % j == 0)
return false;
}
return true;
}
}
● 유클리드 기하학과 택시 기하학
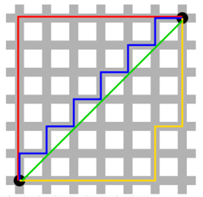

택시 기하학은 D(T1, T2) = |x1 – x2| + |y1 – y2|
빨간 선은 택시 기하학에서의 두 점 사이의 거리이고, 초록 선은 유클리드 기하학에서의 두 점 사이의 거리.
택시 기하학에서의 원의 정의
2 * 2 * R.
<cmath>에서 M_PI 쓸 수 있는데 _USE_MATH_DEFINES 전처리해줘야 함.
택시 기하학은 D(T1, T2) = |x1 – x2| + |y1 – y2|
빨간 선은 택시 기하학에서의 두 점 사이의 거리이고, 초록 선은 유클리드 기하학에서의 두 점 사이의 거리.
택시 기하학에서의 원의 정의
2 * 2 * R.
<cmath>에서 M_PI 쓸 수 있는데 _USE_MATH_DEFINES 전처리해줘야 함.
● 최대공약수와 최소공배수
최대공약수는 유클리드 호제법 사용, 최소공배수는 최대공약수 * 최소공배수 = A * B
int get_gcd(int a, int b){
while (b!=0){
int r = a % b;
a = b;
b = r;
}
return a;
}
int get_lcm(int a, int b, int c){
return a*b/c;
}
● 세 수의 최소공배수 간단하게 구하기
#include <stdio.h>
int main() {
int a, b, c, day = 1;
scanf("%d%d%d", &a, &b, &c);
while (day% a != 0 || day % b != 0 || day % c != 0) {
day++;
}
printf("%d\n", day);
return 0;
}
계속 공부해나가면서 알고리즘과 관련하여 기억해야할 점을 채워나가겠다.
'C++ Programming > 기억해야할 점' 카테고리의 다른 글
| 7. 정렬 다루기 (0) | 2020.05.03 |
|---|---|
| 6. 문자열 다루기 (0) | 2020.05.03 |
| 4. switch문, goto문 (0) | 2020.05.03 |
| 3. shift, bool, 논리 연산자, 3항 연산자 (0) | 2020.05.03 |
| 2. 출력 (0) | 2020.05.03 |