In this class, we will learn about Hough Transform.
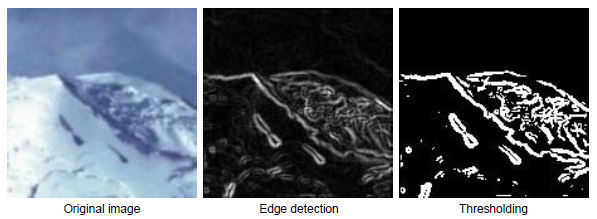
How do we find image boundaries (lines)?
● Hough Transform
- Hough Transform is a generic framework for detecting a shape/object.
- Edges don't have to be connected.
- Lines can be occluded.
- The key idea is 'Democratic' Detector.
→ Each image edge votes for the possible line model.
● Image and parameter space

We can see the image as parameter space.

So, a line in image becomes a point.

And a point becomes a line.

Two points can have one point as common.

Likewise, three points can have one point as common.
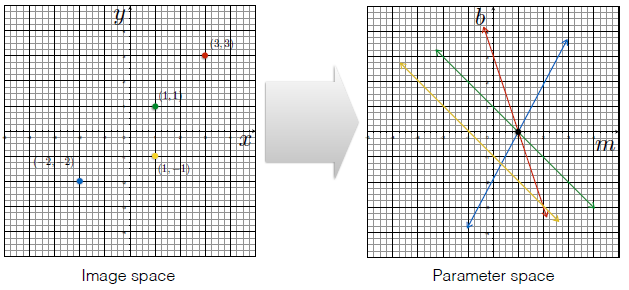
As the number of points increase, possible common points arise.
Is this method robust to measurement noise?
Is this method robust to outliers?
● Line Detection by Hough Transform
Algorithm:
① Quantize Parameter Space (m, c)

② Create Accumulator Array A(m, c)
③ Set A(m, c) for all m, c
④ For each image edge(xi, yi)
For each element in A(m, c)
If (m, c) lies on the line: c = -xim + yi
Increment A(m, c) = A(m, c) + 1

⑤ Find local maxima in A(m, c)

● Problems with parameterization

The problem of parameterization (m, c) is that the space of m and c are huge.
Because m and c range from minus infinity to infinity.
● A better parameterization
For a better parameterization, we should use normal form.
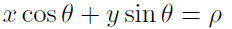
when (xi, yi) is given, we should find (rho, theta).
In this case, rho ranges from 0 to 2pi.
And theta ranges from 0 to rho_max, which is finite accumulator array size.
'AI > Computer Vision Materials' 카테고리의 다른 글
| 5.3 Generalized Hough Transform (0) | 2020.08.07 |
|---|---|
| 5.1 Lines Parameterization (0) | 2020.08.05 |
| 5.0 Defining Boundaries (0) | 2020.08.05 |
| 4.1 Filtering vs Convolution (0) | 2020.08.05 |
| 4.0 Image Gradients and Gradient Filtering (0) | 2020.08.04 |



