이번 시간에는 손실 함수의 최소값을 알기 위해서 사용하는 gradient descent 알고리즘에 대해 알아보도록 하겠다.

저번 시간에 배웠듯이 가중치값을 달리하면서 에러의 평균값들을 알아내서 손실 그래프를 그릴 수 있었다.
우리는 손실 함수의 값을 최소로 하는 가중치를 사용하여 모델을 훈련시키고 싶은 것이다.

그렇다면 이번에는 Linear Regression Error에 대해 알아보도록 하겠다.
위 예에서는 파란 선이 맞는 weight을 사용한 것이므로 우리는 주황색이든 초록색이든 선에서 시작해서 파란선으로 가까이 가게 해야한다.

우리가 해야할 것은 손실 함수를 최소로 하게 하는 가중치 weight을 찾는 것이고, 이것을 pytorch에서는 argmin 함수로 알아낼 수 있다. 위의 arg_w_minloss(w)의 뜻은 우리가 loss(w)을 최소로 하는 weight을 찾고 싶다는 뜻이다.
저번 시간에 한 것처럼 weight을 0, 1, 2 이런 식으로 사람이 일일이 찾는 것 대신 자동으로 찾아내는 gradient descent 알고리즘을 배워보도록 하자.
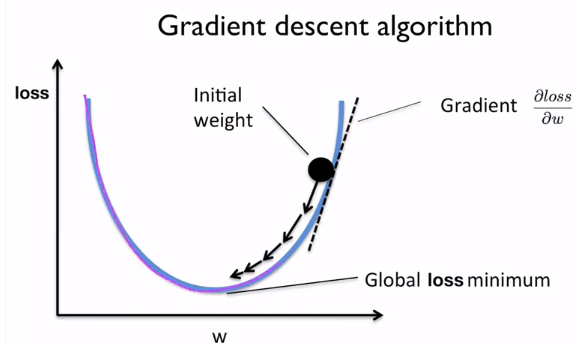
어떤 것이 가장 최적의 가중치인지 처음에는 모르므로 임의의 점에서 시작한다. 우리가 그 이후에 그래프를 따라 왼쪽으로 더 진행할 것인지, 아니면 오른쪽으로 진행할 것인지는 그 지점의 gradient, 기울기를 구해봄으로써 알 수 있다. 이 예시에는 gradient가 +이므로 안쪽으로 진행하게 된다. 만약 위의 그래프에서 w가 0이 가까운 그래프 위의 지점이 시작점이었다고 한다면 기울기가 -이었으므로 오른쪽으로 진행하게 될 것이다.

위의 식을 사용하여 점점 global loss minimum에 점점 다가가게 된다. 위에서 살펴봤듯이 만약 gradient가 +였다면 가중치 값이 최소값에 다다를 때까지 점점 낮아지게 될 것이고, gradient 값이 -였다면 점점 높아지게 될 것이다.
얼마나 움직일 것인지는 alpha에 따라 달려있고 learning rate라고 불리며 보통 매우 작은 값인 0.01이다.

우리가 일단 loss 함수를 결정한다면 어떻게 가중치를 정할 것인지를 결정하게 된 것이다.

여기서 문제는 loss 함수를 weight으로 미분한 값을 어떻게 알 수 있을까?
https://www.derivative-calculator.net/ 사이트를 이용하면 쉽게 구할 수 있다.

맨 처음의 예시에서는 위와 같이 최종적으로 gradient descent 식을 알 수 있었다.

그렇다면 실제로 pytorch에 어떻게 구현할지 알아보자.
위의 예에서는 loss 함수를 w로 미분한 값이 2x(xw - y)이어서 gradient 함수 모양이 저런거지, 본인의 손실 함수에 적용하려면 식을 그에 맞춰서 바꾸면 된다.

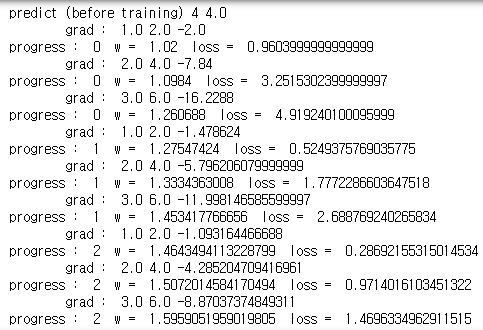

가중치 갱신은 방금 정의했던 forward, loss, gradient 함수로 가능하다. 현재의 학습률은 0.01로 설정했다.
epoch는 에폭으로 읽고 얼마나 반복할지를 결정하고, 이 경우에는 0부터 99까지 100번 3개의 데이터에 대해서 반복했다. 시간이 지날수록 loss가 점점 줄어드는 것을 볼 수 있고 그만큼 더 알맞은 가중치의 값으로 다가가고 있다.
처음에는 초기 가중치 값이 임의로 설정된 1.0이었고, 4시간을 공부한다면 4.0점을 받을 것이라고 예측했지만, 100버능의 학습을 한 뒤에는 7.9정도의 점수를 받을 것이라고 예측하게 되고 정답은 8이므로 맞다고 할 수 있다.

마지막으로 가중치가 여러 개 있을 때에는 어떻게 gradient를 계산해야하는지 생각해보자.
각 가중치에 대해서 따로 손실 함수를 미분해야한다.
다음 시간에는 이런 gradient를 graph를 이용해서 자동으로 구하는 방법을 알아보겠다.
'AI > PyTorchZeroToAll by Sung Kim' 카테고리의 다른 글
| [PyTorchZeroToAll] 6. Logistic Regression (0) | 2020.01.23 |
|---|---|
| [PyTorchZeroToAll] 5. Linear Regression in the PyTorch way (0) | 2020.01.22 |
| [PyTorchToAll] 4. Back-propagation (0) | 2020.01.22 |
| [PytorchZeroToAll] 2. Linear Model (0) | 2020.01.21 |
| [PyTorchZeroToAll] 1. Overview (0) | 2020.01.20 |



