저번 시간에는 데이터가 무엇인지, 어떤 종류가 있고 어떤 특성들을 가지고 있는지에 대해 배웠다.
이번 시간에는 데이터 전처리에 대해 알아보도록 하겠다.
1. Aggregation (집단화)
- 두개 혹은 그보다 많은 attribute나 object를 하나의 attribute 또는 object로 합치는 것이다.
- 2개 이상의 attribute를 하나의 attribute로 몬 것이 아니고, 여러 개의 object를 한 개의 값으로 변환하는 것이다.
→ 평균, 분산 등 데이터 여러 개를 하나로 종합한다는 뜻.
- 예: 여러 데이터에 나이라는 속성값이 있으면 평균으로 하나의 값으로 일반화할 수 있다.
* 목적
① Data reduction
- attribute나 object의 수를 줄인다
② Change of scale
- 예를 들어, cities를 regions, states, countries등으로 종합한다.
③ More "stable" data
- 데이터의 noise를 제거함으로써 좀 더 안정적인 값이 될 수 있다.
- aggregated data tends to have less variability
예: 오스트레일리아의 강우량 변화
- 강우량이 매일매일 기록되는데 월별로, 연별로 평균을 낸다.
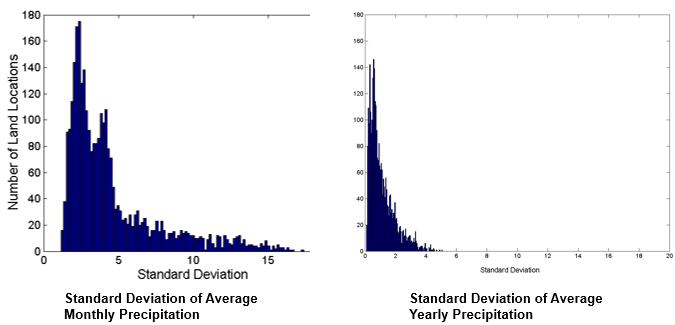
2. Sampling (표본 추출)
- 데이터가 굉장히 많은 경우에 그 중에서 일부를 랜덤하게 추출함으로써 데이터의 사이즈를 줄인다.
- 샘플링을 하는 이유는 데이터의 사이즈가 너무 크기 때문에 그 모든 데이터들을 처리하는 데 너무 많은 시간이 들고
처리 비용이 너무 비싸기 때문이다.
- 통계적으로도 sampling하는 게 의미가 있다.
→ 오류 없이도 유의미한 결과를 얻을 수 있다.
* 효과적인 Sampling의 원칙
- 표본을 사용하는 것은 그 표본이 전체 데이터셋을 대표한다면 (representative), 전체 데이터셋을 쓰는 것과
같은 효과를 낼 것이다.
- 표본은 원본 데이터와 거의 같은 속성을 가질 때 representative하다.
* Sampling의 종류
① Simple Random Sampling
- 전체 중 어떤 원소를 뽑을 확률이 모두 같다.
- 아무렇게나 랜덤하게 뽑는다.
② Sampling without replacement
- 모집단에 안 넣겠다. 한 번 샘플링된 것은 다음 번에 또 샘플링될 가능성이 없다.
③ Sampling with replacement
- 샘플링한 것을 모집단에 다시 넣어서 그게 다음에 샘플링이 또 될 가능성이 0이 아니다.
→ ②, ③은 랜덤 샘플링한 것은 똑같고 그 다음에 샘플링하기 이전에 방금 샘플링한 것을 모집단에 집어넣느냐
안 넣느냐 차이이다.
④ Stratified sampling (지칭적 샘플링)
- 데이터의 분포를 보고 그 분포의 특성에 맞게 샘플링하는 것.
- 데이터의 밀도가 많은 곳에서는 좀 많이 뽑고, 밀도가 낮은 곳에서는 덜 뽑기
- 데이터의 밀도가 낮은 곳에서 오히려 더 뽑을 수도 있다.
- 어쨋든 밀도에 의해 차이를 두는 것.
* Sample Size
- 샘플링된 데이터의 크기에 따라서 전체의 윤곽의 선명도가 달라진다.
- 샘플링을 많이 할수록 원본 데이터에 가까워진다.

- 그렇다면 우리가 통계적으로 유의미한 결과를 얻기 위해서 샘플 크기를 얼마로 해야할까?
- 예: 모집단에 10개의 그룹이 있는데 각 그룹 안에 있는 데이터를 랜덤으로 샘플링해서 10개의 그룹에서 적어도
하나씩 데이터가 나올 확률?
→ 이것이 0이 되지 않으려면 샘플 사이즈가 얼마정도 되어야하는가?

- 위의 표를 본다면 60개 정도 샘플링하면 거의 99%의 확률이 나오는 것을 볼 수 있다. 만약 30개를 샘플링한다면
10개 그룹 중 4개 그룹 정도는 안 뽑힐 수 있다.
* Curse of Dimensionality (차원의 저주 현상)
- attribute 개수가 차원의 크기인데 만약 data의 attribute 개수가 n개라고 한다면 그 데이터를 n차원 공간의 한 점으로 표시할 수 있다. 그 때 n이 점점 커질수록 분석하기 어려워지는 현상이 나타난다.
- 최소 거리와 최대 거리의 차이가 최소거리의 몇 배나 되는지 log 스케일로 나타내면 아래와 같다.

- 랜덤하게 500개의 포인트를 추출하고 어떤 두 점 사이든 최대 거리와 최소 거리를 계산한다.
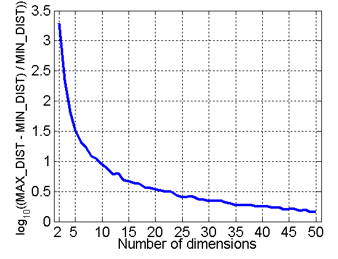
- 거리가 다들 비슷해져서 데이터가 유사하다, 유사하지 않다라는 판단 기준이 애매해진다.
→ outlier detection도 어려워지고 clustering도 어려워져서 분석하는 데 어려워진다.
- clustering같은 것을 할 때 data 사이의 거리로 similarity를 계산하는데 거리가 가까우면 유사도가 높고 멀면 낮다.
→ 차원이 점점 커질수록 0에 가까워진다.
→ max와 min의 차이가 점점 줄어든다.
→ 모든 데이터가 비슷한 거리에 분포한다.
3. Dimensionality Reduction (차원 축소)
* 목적
- 차원이 커지면 분석이 어려워지는 차원 저주 현상 막기
- 데이터마이닝 알고리즘들에 필요한 시간과 공간의 양 감소
- 데이터들을 잘 시각화하기
→ 시각화는 최대 3차원까지밖에 안 된다. 그 이상은 안 돼서 2, 3차원으로 줄여야한다.
- 부적절한 특성들을 없애거나 noise를 줄이는 데 도움을 준다.
* 사용 기술들
- 주성분 분석 (PCA : Principal Component Analysis)
- Singular Value Decomposition
- Others : supervised and non-linear techniques
* PCA (Principal Component Analysis)
- 데이터들이 어떤 방향으로 주로 모여있는지에 대한 측정을 할 수 있다.
- 데이터들은 다차원 공간의 한 점으로 나타내면 실제 데이터의 분포는 다차원 공간 안에서 저차원 공간의 subspace를
차지하게 되는 것이 일반적이다.

- 예: 2차원 점들이 위와 같이 있으면 오른쪽 위로 항하는 방향의 데이터의 variation이 왼쪽 위로 향하는 방향보다 크다.
그래서 주성분은 오른쪽 위를 향하는 방향이 된다. 이것을 1차원으로 축소시키려면 variation이 작은 왼쪽 위를 향하는
방향은 무시하는 것이다.
- 구체적으로 수치화해서 구하는 방법은 covariance matrix의 eigen vector를 구하는 것이다.
- covariance matrix에서 eigen vector와 eigen value를 구하면 eigen vector는 2개(오른쪽 위를 향하는 방향, 왼쪽 위를
향하는 방향), 그리고 각각에 eigen value(그 길이)가 주어진다.
→ 이 중에서 eigen value가 큰 eigen vector를 구하면 그것이 주성분이 되는 것이다.
- 이 경우에는 attribute가 2개, 그래프에서 보면 X1, X2 attribute가 있는 것이다.

* ISOMAP

- neighborhood graph를 그린다
- 그래프의 각 두 점에서 최단거리를 구한다 - geodesic distances
- by Tenenbaum, de Silva, langford (2000)
- 차원 축소의 문제점 : 차원 축소를 하면 정보 손실이 반드시 발생한다.
→ 차원이 커질수록 정보 손실이 덜 발생하므로, 적당한 차원 크기를 정해야한다.
4. Feature Subset Selection
- attribute 중 새로운 attribute를 만드는 것이 아니라 일부 attribute를 선택하는 것
- 차원 축소를 하는 또다른 방법
① Redundant features
- 하나 이상의 attribute에서 중복된 데이터가 포함되어있을 수 있다.
- 예: 제품의 구매 가격과 지불된 판매 세금의 양
→ 세금은 가격에 비례하기 때문에 redundant한 feature로 판단될 수 있다.
→ 둘 중에 하나를 삭제하면 된다.
② Irrelevant features
- 부적절한 특성들
→ 중복되어있는 건 아닌데 데이터마이닝 태스크를 할 때 별로 유용한 정보를 주지 못하는 속성들
- 예: 어떤 학생의 성적을 예측하는 태스크가 있다면 각각의 과목의 성적, 각각의 과목의 유사성 이런 게 중요한 것이지,
각 학생의 학번이 중요하지는 않다.
* Feature Selection 사용 방법들
① Brute-force approach
- 데이터마이닝 알고리즘의 입력으로 모든 가능한 특성 부분집합을 넣어본다.
② Embedded approaches
- 데이터마이닝 알고리즘의 부분으로 feature selection이 자동적으로 수행된다.
③ Filter approaches
- 데이터마이닝 알고리즘이 실행되기 전에 feature들이 선택된다.
④ Wrapper approaches
- 데이터 마이닝 알고리즘을 속성들의 최선의 부분집합을 찾기 위한 블랙박스로 사용한다.
5. Feature Creation
- 기존 attribute보다 데이터에서 정보를 더 효율적으로 뽑아낼 수 있는 새로운 attribute를 만든다.
* 가장 일반적인 세 방법
① Feature Extraction
- domain-spacific
② Mapping Data to New Space
③ Feature Construction
- combining features
* Mapping Data to a New Space
① Fourier transform
② Wavelet transform
- 이런 변환 방법들을 사용한다. 어떤 데이터가 일정 주기를 가지고 있으면 거리 domain의 데이터를 주파수 domain의 데이터로 변환시킴으로써 데이터의 사이즈를 많이 줄일 수 있다.

6. Discretization Using Class Labels (이산화)
- Entropy based approach
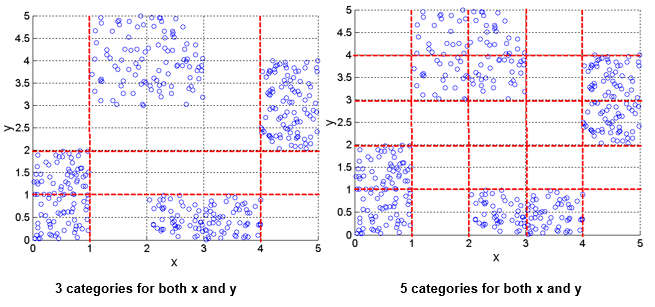
- x, y attribute는 실수이다.
- attribute들이 실수값을 가지면 분석하기 어려울 수 있다. 그래서 이것을 discretization(이산화)를 할 필요가 있다.
→ 그렇다면 이것을 어떻게 나눠야할지라는 문제가 생긴다. class label을 가지고 entropy라는 개념을 사용하며,
entropy가 최소화되는 방향으로 데이터들을 나눈다.
* 클래스 레이블 없이 이산화하는 방법
- 원본 데이터

→ 여기서 x축은 어떤 attribute의 값이고, y축은 그 값이 얼마나 많이 분포하는가(빈도)를 뜻한다.
① Equal Interval Width
- 구간의 길이를 똑같이 둔다.
- 이 경우에는 4개의 구간을 만들어서 그 중간 구간에 몇 개나 있는지 센다.
→ 쉽게 나눌 수 있기 때문에 시간이 적게 걸리는 방법
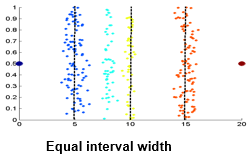
② Equal Frequency
- 20개의 값을 4개로 축소하기 위해서 구간을 구간 안에 들어가는 데이터의 개수가 같도록 나누는 방법
→ 개수를 다 세야하기 때문에 시간이 많이 걸린다.

③ K-means
- 데이터의 개수를 똑같이 하는 게 아니라 데이터를 clustering하는 것.
- 데이터들 가운데 가까운 것을 cluseter에 넣다보면 된다.
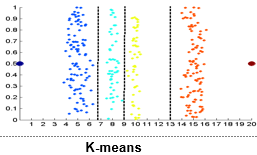
- 대부분의 경우 equal frequency가 equal width보다 더 유의미한 결과를 보인다. 하지만 equal frequency는 count가
필요해서 시간이 많이 걸린다.
7. Attribute Transformation
- 어떤 attribute의 값에 대응되는 다른 attribute의 값을 변화하는 것
- 보통은 시계열 데이터에서 많이 사용된다. 시간이 지남에 따라 주가, 기온, 압력 등 값이 어떻게 변화하는지 볼 때
쓰인다.
- 가장 간단하게 쓰이는 함수들은 아래와 같다.
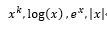
- 또는 표준화(standardization)과 정규화(normalization)가 쓰이기도 한다.
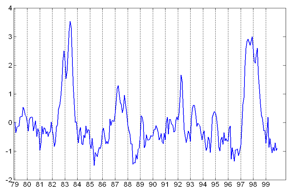
- 위 그래프는 시간에 따라 x값이 편화하는 모습을 보이는 정규화된 그래프이다.
- 정규화는 평균(m)과 표준편차를 이용하여 평균이 1이고 표준편차가 1인 정규분포 N(0, 1)로 바꾸는 것이다.
→ x 값을 z로 변환하는 것이다.
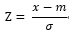
다음 시간에는 데이터들 간에 simalarity와 dissimalarity를 계산하는 방법들을 알아보도록 하겠다.
'CS > Data Mining' 카테고리의 다른 글
| [DataMining] Deep Learning (1) | 2020.05.03 |
|---|---|
| [DataMining] AI & Machine Learning (0) | 2020.05.03 |
| [DataMining] 1-2. Data Mining Tasks (0) | 2020.04.27 |
| [DataMining] 1-1 . Introduction to Data Mining (0) | 2020.04.27 |



