
이번 시간에는 파이토치를 이용하여 가장 기본적인 인공 신경망인 ANN(Artificial Neural Network)을 구현해보도록 하겠다. 구체적으로는 텐서와 Autograd 패키지, 경사하강법으로 이미지 복원하기, 신경망 모델 구현하기를 해볼 것이다.
파이토치가 행렬 계산이 많은 딥러닝의 특성을 담아서 파이썬과 조금 다르다. 텐서(tensor)가 가장 기본적인 자료구조로서 그 예이다.
※ 3.1 텐서와 Autograd
● 3.1.1 텐서의 차원 자유자재로 다루기
⊙ 파이토치 임포트

⊙ 텐서
텐서는 파이토치에서 다양한 수식을 계산하는 데 사용하는 가장 기본적인 자료구조이다. 수학의 벡터나 행렬을 일반화한 개념으로, 숫자들을 특정한 모양으로 배열한 구조이다.
텐서에서 중요한 개념은 차원, 랭크(rank)이다. 랭크가 1이면 스칼라(scalar), 2이면 2차원 행렬(matrix), 3이면 3차원 행렬, 랭크 n 텐서는 3차원 이상이다.
예를 들자면 다음과 같다
1 → 스칼라. 모양은 []
[1,2,3] → 벡터. 모양은 [3]
[[1,2,3]] → 행렬. 모양은 [1, 3]
[[[1,2,3]]] → n랭크 텐서. 모양은 [1,1,3]
이런 성질을 가지고 있는 텐서를 pytorch에서 직접 다뤄보도록 하겠다.
먼저 torch.tensor([...]) 함수를 이용하여 tensor를 선언한다.

위의 코드는 가로와 세로 2차원으로만 이루어진 랭크 2 텐서이다.

⊙ size(), shape, ndimension()
이런 함수들을 사용해서 크기, 모양, 차원을 알 수 있다.

⊙ unsqueeze()
unsqueeze 함수는 텐서 x의 랭크를 늘릴 수 있다. 위 코드는 [3, 3] 형태의 랭크 2 텐서의 첫 번째(0번째) 자리에 1이라는 차원값을 추가해 [1,3,3] 모양의 랭크 3 텐서로 변경했다. 랭크는 늘어나도 텐서 속의 원소의 수는 유지되는 것에 주의하자.
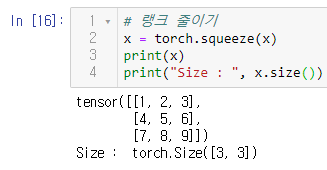
⊙ squeeze
squeeze() 함수는 텐서의 랭크 중 크기가 1인 랭크를 삭제하여 다시 랭크 2 텐서로 되돌릴 수 있다. 아까의 코드에서 크기가 1인 랭크를 삭제하여 다시 [3, 3] 모양으로 되돌아간 모양이다.

크기가 1인 랭크가 shape의 맨 마지막이더라도 삭제되는 것을 볼 수 있다. 텐서의 원소의 개수는 그대로이다.

크기가 1인 랭크가 여러 개이면 그것들을 모두 삭제한다. 역시나 텐서의 총 원소 수는 그대로이다.

가운데가 1이어도 그것만 삭제한다. 역시나 텐서의 총 원소 수는 그대로이다.
⊙ view
view() 함수는 위의 작업들을 쉽게 할 수 있을 뿐만 아니라, 텐서의 모양을 바꿀 수도 있다. 랭크 2의 [3, 3] 모양인 x를 랭크 1의 [9] 모양으로 바꿔보도록 하겠다.



3 * 3 * 3의 행렬일 때에도 마찬가지이다.

꼭 1차원이 아니더라도 위와 같이 모양을 바꿀 수 있다.
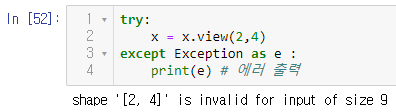
만약 view로 바꾸려는 모양의 총 원소 개수가 원래의 텐서와 다르다면 바꿀 수 없다. 에러 메시지를 출력하는 try~ except 형태도 기억해두자.
● 3.1.2 텐서를 이용한 연산과 행렬곱
행렬과 행렬곱은 모든 딥러닝 알고리즘에 사용되므로 처음부터 제대로 알아놓는 것이 좋다. 앞에서 이미 짚고 넘어갔듯이 행렬은 랭크 2 텐서와 같은 개념이고, 숫자들을 네모꼴로 배치한 2차원 배열이다.
수학 시간에 기본으로 배웠듯이 A · B의 형태의 행렬곱을 하려면 다음 두 가지 조건이 성립해야 한다.
-A의 열 수와 B의 행 수는 같아야 한다.
-행렬곱 A · B의 결과 행렬의 행 개수는 A와 같고, 열의 개수는 B와 같다.
이제 파이토치로 이 행렬곱을 구현해보자.
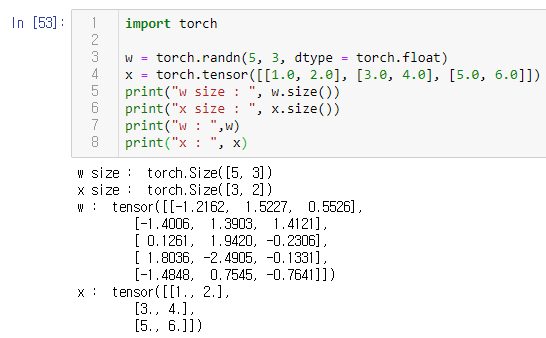
위에서 정의한 행렬 w 부분은 정규분포(normal distribution)에서 무작위로 값을 뽑아 텐서를 생성하는 randn() 함수에 5와 3을 인수로 전달하여 5 x 3의 shape을 가진 텐서를 만드는 것이다. 처음 두 인수는 행과 열의 개수이고, 세번째 인수는 값의 타입이다. 무작위로 값을 뽑을 때 실수의 범위 내에서 뽑도록 randn() 함수의 인수 dtype에 torch.float을 지정한다. 랜덤 함수를 사용하기 때문에 실행할 때마다 결과가 달라질 것이다.
행렬 x의 경우는 직접 실수형 원소들을 넣어 3 x 3의 shape를 가진 텐서를 정의한다.
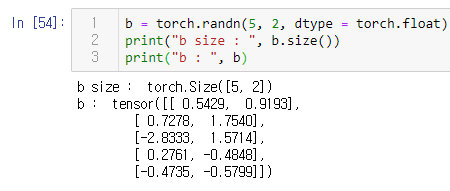
행렬곱 외에도 다른 행렬 연산에 쓰일 b라는 텐서도 추가로 정의한다.
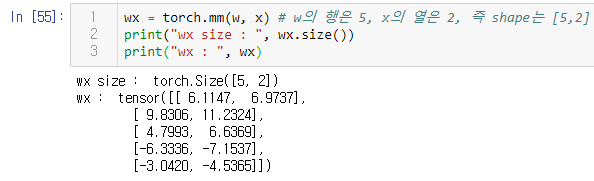
행렬곱은 torch.mm() 함수로 수행한다.

행렬곱 수행 이후에 역시 5, 2 크기의 행렬인 b를 더해주는 것도 가능하다.
● 3.1.3 Autograd
Autograd는 수식의 기울기를 자동으로 계산한다. 머신러닝 모델은 입력된 데이터를 기반으로 학습을 하기 때문에 데이터가 충분하지 않으면 모델은 올바르지 않은 답을 예측할 수도 있다.
거리(distance)는 데이터에 대한 정답 (ground truth)과 머신러닝 모델이 예측한 결과의 차이를 산술적으로 표현한 것이다.
오차(loss)는 학습 데이터로 계산한 거리들의 평균이다. 오차가 작은 머신러닝 모델일수록 주어진 데이터에 대해 더 정확한 답을 낼 수 있다.
경사하강법(gradient descent)는 오차를 최소화하기 위해 가장 유명하고 많이 쓰이는 알고리즘으로, 오차를 수학 함수로 표현한 후 미분하여 이 함수의 기울기(gradient)를 구해 오차의 최솟값이 있는 방향을 찾아내는 알고리즘이다. 복잡하지 않은 모델이라면 numpy 등의 라이브러리로 경사하강법을 쉽게 구할 수 있지만 복잡한 인공 신경망 모델에서는 여러 번 계산을 해야한다.
경사하강법에 대한 부가 정보는 이찬우님의 영상 '[딥러닝] 2. 선형회귀와 Gradient Descent' 유튜브 강의를 참고하면 된다. https://youtu.be/GmtqOlPYB84
파이토치의 경우에는 Autograd가 있어서 미분 계산을 자동으로 해주어서 경사하강법을 좀 더 편하게 구현할 수 있다. 예를 들어서 Autograd를 구현해보도록 하겠다.

값이 1.0인 스칼라 텐서 w를 정의하고, 수식을 w에 대해 미분하여 기울기를 계산할 것이다. w의 requires_grad를 True로 설정하면, 파이토치의 Autograd 기능이 자동으로 계산할 때 w에 대한 미분값을 w.grad에 저장한다.
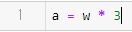
3을 곱한 후 제곱을 하는 최종 연산을 하려고 했다고 친다면 다음으로는 a = w * 3을 정의했다.

위와 같이 backward를 수행한다.
※ 3.2 경사하강법으로 이미지 복원하기
파이토치는 이전에 설명한 것과 같이 학습과 최적화 알고리즘을 제공하지만, 이번에는 최적화를 직접 구현해보자.
● 3.2.1 오염된 이미지 문제
오염된 이미지가 생긴 다음과 같은 예시를 생각해보자. weird_function() 함수에 버그가 들어가서 이미지 처리가 잘못되어 100 x 100의 잘못된 이미지가 만들어졌다. 원본 이미지가 삭제되어버려서 이 오염된 이미지와 소스 코드를 사용하여 원본 이미지를 복원해보자.
● 3.2.2 오염된 이미지를 복원하는 방법
보통 사람이라면 weird_function을 분석하여 했던 동작들을 반대로 하는 방법을 생각할 것이다. 그런데 이것은 코드 한 줄 한 줄을 완벽하게 이해하고 배경 지식도 있어야하기 때문에 복잡하고 어려울 수 있다.
그렇기 때문에 우리가 사용할 방법은 다음과 같다.
① 오염된 이미지(broken_image)와 크기가 같은 랜덤 텐서(random_tensor)를 생성한다.
② 랜덤 텐서를 weird_function() 함수에 입력해 똑같이 오염된 이미지를 가설(hypothesis)이라고 한다.
③ 가설과 오염된 이미지가 같다면, 무작위 이미지와 원본 이미지도 같을 것이다.
④ 그러므로 weird_function(random_tensor) = broken_image 관계가 성립하도록 만든다.
위 가정에서 오차는 가설과 원본 이미지가 weird_function() 함수를 통해 오염되기 전의 이미지(정답) 사이의 거리일 것이다. 그렇기 때문에 이 오차가 최소값이 되는 랜덤 텐서를 구하기 위해서 우리는 계속 움직여야한다. 이렇게 랜덤 텐서를 미분값의 반대 방향으로 조금씩 이동하면서 모델을 최적화하는 것이 경사하강법 알고리즘이다.
● 3.2.3 문제 해결과 코드 구현
위에서 언급한 문제를 해결하기 위해서 직접 코드를 구현해보도록 하겠다.
pytorch를 임포트한 뒤, 오염된 이미지와 복원된 이미지를 출력하기 위해서 matplotlib을 사용한다. pickle 라이브러리는 오염된 이미지 파일을 로딩하는 데 사용될 것이고, 피클은 파이썬 객체를 파일 형태로 저장할 때 쓰는 파이썬에서 제공하는 기본 패키지로, 별도의 설치 없이 사용 가능하다.

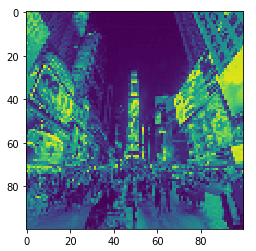
오염된 이미지를 파이토치 텐서의 형태로 읽으면 픽셀값들을 숫자로 늘어놓은 행렬로 표현된다. matplotlib로 100 x 100 형태로 바꾼 후 시각해보면 아래와 같다.


이미지를 오염시킨 함수는 위와 같다. 위에서 언급한 것과 같이 이 코드 한 줄 한 줄을 이해하고 거꾸로 하지 않을 것이기 때문에 이 코드를 자세히 볼 필요는 없다.

가설 텐서와 오염된 이미지 사이의 오차를 최소화하는 것이 우리의 목표에 맞는 방향일 것이다.
여기서 torch.dist()는 두 텐서 사이의 거리를 구한다.

무작위 텐서를 생성한다. 이 텐서를 경사하강법을 이용해서 점점 원본 이미지에 가깝게 만들 것이고, 이것은 [100, 100] 모양의 행렬이 [10000] 모양의 벡터로 표현된 형태이다. lr은 learning rate, 학습률을 나타내는 것으로 경사하강법에서 얼마만큼씩 하강할 것인지를 나타낸다.

본격적으로 경사 하강법을 구현해보겠다. 오차 함수를 random_tensor로 미분해야하므로 reauires_grad를 True로 설정하고, 랜덤 텐서를 weird_function()에 통과시켜서 가설을 구한다. distance_loss 함수로 오차를 구하고 loss.backward() 함수로 loss를 랜덤 텐서로 미분한다. 여기서 torch.no_grad()는 파이토치의 자동 기울기 계산을 비활성화해서 우리가 직접 구현하는 경사하강법이 작동하도록 한다. 그 이후에는 점점 loss가 작아지는 방향으로 학습률만큼씩 내려간다. for문이 1000번 반복할 때마다 오차를 출력하도록 하겠다.

마지막으로 복원된 이미지를 출력하겠다. 복원된 이미지는 뉴욕 타임스퀘어의 이미지였다. 직접 실행해본다면 반복문의 횟수가 적으면 덜 복원이 되는 것을 알 수 있다.



전체 코드는 위와 같고, 결과가 점점 작아지면서 원본 이미지에 가까워진다.
※ 3.3 신경망 모델 구현하기
● 3.3.1 인공 신경망(ANN)
인공 신경망(ANN : artificial neural network)은 인간의 뇌, 신경계의 작동 방식에서 영감을 받았다. 눈 등의 감각 기관을 통해 자극을 입력받고, 신경세포들을 거치면서 각 자극에 따라 다른 반응을 보인다. 우리의 인공 신경망에서는 자극을 입력받는 감각 기관에 해당하는 부분을 입력층(input layer)이라고 하고, 이 자극들은 은닉층(hidden layer)을 거쳐서 마지막 뉴런인 출력층(output layer)에 다다른다. 각 층에 존재하는 한 단위의 인공 뉴런은 노드라고 한다.
인접한 층으로 전달하기 전 가중치(weight)에 행렬곱을 하고, 편향(bias)을 더해줘서 전달한다. 가중치는 입력 신호가 출력에 주는 영향을 계산하는 매개변수이고, 편향은 각 노드가 얼마나 데이터에 민감한지 알려주는 매개변수이다.
이 행렬곱의 결과는 활성화 함수(activation function)을 거쳐서 인공 뉴런의 결과값을 산출하고, 이 활성화 함수는 입력에 적절한 처리를 해서 출력 신호를 변환하는데, 입력 신호의 합이 활성화를 일으키는지 아닌지를 정하는 것이다.
이렇게 인공 신경망의 예측을 얻었다면 정답과 오차를 계산해서 더 완벽한 결과를 내도록 모델을 수정해야 한다. 이 오차를 기반으로 경사하강법을 활용하여 가중치를 출력에서부터 입력까지 뒤에서 앞으로 거꾸로 가면서 차례로 조정해야하고, 이것을 역전파 알고리즘(backpropagation)이라고 한다.
● 3.3.2 간단한 분류 모델 구현하기
분류(classification)을 수행하는 간단한 모델을 구현해보도록 하겠다.

numpy는 수치해석용 라이브러리로, 행렬과 벡터 연산에 아주 유용하며, 파이토치도 이 넘파이를 이용해 개발되었을 정도로 머신러닝에서 많이 사용된다. sklearn(사이킷런)은 파이썬의 대표적인 머신러닝 라이브러리고, matplotlib으로 학습 데이터의 분포와 패턴을 시각화하겠다.

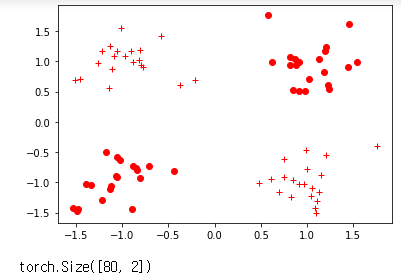
다음으로는 모델에 넣을 데이터셋을 만들겠다. x_train은 훈련 입력 데이터, y_train은 훈련 정답 데이터, x_test는 시험용 입력 데이터, y_test는 시험용 정답 데이터이다. 여기서 쓰인 make_blobs는 사이킷런에 있는 함수로, 데이터를 2차원 벡터 형태로 만들 수 있다. 이 경우에는 학습 데이터셋에 80개, 실험 데이터셋에 20개의 2차원 벡터 데이터가 있다. 이 함수에서의 레이블 데이터는 각 데이터 하나하나가 몇 번째 클러스터에 속해있는지 알려주는 인덱스이다. 이번에는 4개의 클러스터가 있고, 각각은 0,1,2,3으로 표시된다.

데이터를 만든 다음에는 각 데이터에 정답 레이블을 달아줄 것이다. make_blobs 함수에서 이미 인덱스 레이블을 만들어냈고, 우리의 예시에서는 두 가지 레이블만 예측하기 때문에 4개의 레이블을 2개로 합칠 것이다.
label_map이라는 함수는 0번 혹은 1의 레이블을 가진 함수를 0번 레이블로 합치고, 2번과 3번 레이블을 가진 데이터는 1로 합친다.

vis_data 함수는 데이터가 제대로 만들어지고 레이블링됐는지 matplotlib 라이브러리를 활용하여 시각적으로 확인할 수 있다.

이전에 생성한 데이터들을 pytorch tensor로 변환한다.

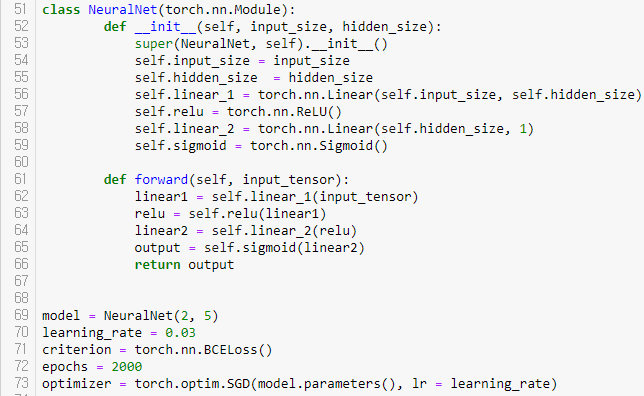
신경망 모델을 구현하겠다. 파이토치에서는 신경망 모듈(torch.nn.Module)을 통해서 신경망을 구현한다. __init__함수에서는 초기화를 하는데, 객체를 만들면 자동으로 호출된다. super의 역할은 우리가 만든 NeuralNet 클래스가 파이토치의 nn.Module 클래스의 속성들을 가지고 초기화하게 한다. torch.nn.Linear 함수는 행렬곱과 편향을 포함하는 연산을 지원하는 객체를 반환하고, linear_1과 linear_2 함수를 거친 이후에 각각 relu와 sigmoid 함수를 사용한다. ReLU 함수는 입력값이 0보다 작으면 0을 반환하고, 0보다 크면 1을 반환한다. ReLU를 통과한 뒤 linear_2의 행렬곱을 거친 다음 sigmoid 함수를 통해서 0과 1 사이의 임의의 수를 결과로 내서 0과 1 중 어디에 가까운지 알 수 있다.

입력 데이터 개수가 2이고, 출력 데이터 개수가 5인 모델을 만들고 학습률은 0.03, 오차 함수는 이진 교차 엔트로피(binary cross entropy)를 사용하겠다.

epoch(이폭)은 전체 학습 데이터를 총 몇 번 모델에 입력할지 결정하는데, 이폭을 너무 작게 설정하면 모델이 충분히 학습되지 않을 수 있고, 너무 크게 설정하면 모델 학습이 너무 오래 걸리므로 적당한 크기로 설정해야 한다.
여기서 학습에 사용할 최적화 알고리즘으로 확률적 경사하강법(stochastic gradient descent, SGD)을 사용했고, 이전 예제에서 이미지 복원에 사용한 최적화 방법과 비슷하다. 새 가중치 = 가중치 - 학습률 X 가중치에 대한 기울기의 형태이다. 파이토치에서 제공하는 optim.SGD 클래스를 사용하여 간편하게 optimizer을 만들 수 있다.
optimizer은 step() 함수를 부를 때마다 가중치를 학습률만큼 갱신하고, model.parameters() 함수로 추출한 모델 내부의 가중치와 학습률을 입력할 수 있다.

학습을 하지 않은 모델의 성능을 시험해보는 코드이다. squeeze 함수를 호출해서 모델의 결과값과 레이블값의 차원을 맞추고 오차를 구한다. item() 함수는 텐서 속의 숫자를 스칼라 값으로 반환하고 test_loss_before가 텐서의 형태이므로 item()으로 오차를 나타내볼 수 있다.
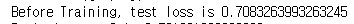
학습 전에는 오차가 약 0.71인 것을 알 수 있다. 100개 중 71번 정도가 틀린다는 뜻이므로 거의 분류를 못한다.
모델에 train() 함수를 호출해 학습 모드로 바꿔주고, 이폭마다 새로운 경사값을 계산할 것이므로 zero_grad() 함수를 호출해 경사값을 0으로 초기화한다. 그리고 x_train의 학습 데이터를 입력해서 결과값을 계산한다.

결과값의 차원을 레이블의 차원과 같게 만들고 오차를 계산한 뒤 100 이폭마다 오차를 출력해서 학습이 잘 되는지 확인한다. 오차 함수를 가중치로 미분하여 오차가 최소가 되는 방향을 구하고, 그 방향으로 모델을 학습률만큼 이동시킨다.

이렇게 오차를 점점 줄일 수 있다.


학습 전과 비교해서 0.71에서 0.36 정도로 오차가 많이 줄어들어서 더 나은 예측을 하는 것을 볼 수 있다.

학습된 모델을 state_dict() 함수 형태로 바꾼 뒤 .pt 파일로 저장한다. state_dict() 함수는 모델 내 가중치들이 딕셔너리 형태로 { 연산 이름 : 가중치 텐서와 편향 텐서}와 같이 표현된 데이터이다.


model.pt로 저장된 파일을 불러서 이미 학습된 모델의 가중치를 곧바로 적용할 수 있다. 새로운 모델인 new_model을 생성하고 앞서 학습된 모델의 가중치를 입력한다. 새로운 모델에 벡터 [-1,1]을 입력하면 레이블이 1일 확률이 94%나 되고, 첫번째 신경망 모델임을 생각하면 분류 정확도가 높은 것을 알 수 있다.






전체 코드와 결과는 위와 같다.
'AI > 펭귄브로의 3분 딥러닝 파이토치맛' 카테고리의 다른 글
| [3분 딥러닝] 4. 패션 아이템을 구분하는 DNN (0) | 2020.01.28 |
|---|---|
| [3분 딥러닝] 5. 이미지 처리 능력이 탁월한 CNN (1) | 2020.01.28 |
| [3분 딥러닝] 1. 딥러닝과 파이토치 (0) | 2020.01.21 |


