[DLBasic]Lecture 3 . How to minimize cost

     저번 시간에 설명했던 cost function을 어떻게 최소화해서 Linear Regression을 완성할 것인지가 이번 시간의 중요 포인트가 되겠다.

 

Simplified Hypothesis

     b를 없애서 간단하게 가정한다고 하고, cost function도 역시 b를 없애서 위와 같이 간략하게 가설을 세웠다고 하자. 최소화하는 값인 W를 찾고자 한다.

cost function의 예

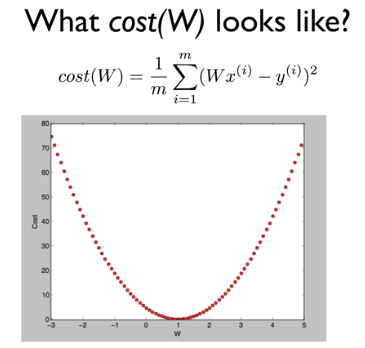
     예를 들어 위와 같이 cost function을 그릴 수 있겠다. 여기서 cost function이 최소화되는 점은 0이다.

이 최소화되는 점을 찾기 위해서 가장 많이 사용되는 방법은 'Gradient Descent Algorithm'이다.

경사를 따라 내려가는 알고리즘이라고 할 수 있겠고, cost function을 최소화하는 점을 찾는 데 사용되고, 이외에도 많은 minimization 문제들에 사용된다고 한다. W1, W2...등 많은 값들이 있는 cost function에서도 최소값을 찾을 수 있는 아주 좋은 알고리즘이다.

     경사가 있는 쪽으로 일정한 크기만큼 계속 내려가다가 최소값을 찾는 방법이다. 만약 5에서 출발하고 간격이 1이라고 한다면 5,4,3,2,1,0 순으로 최소값인 0에 다다르게 된다.

     아무 점에서 시작할 수도 있고, W를 조금씩 바꿔서 그 때의 경사도를 계산해서 cost function이 최소가 되는 점을 찾는다. 항상 최소값을 찾을 수 있다.

미분 사용

     미분을 사용해서 formal하게 cost function에서 minimum 값을 구해보겠다.

미분으로 cost function의 최소값 구하기 

     여기서 alpha는 learning rate이다. 기울기를 구해서 가장 작을 때를 구한다.

W를 계속 변화시키면서 실험

     W를 계속 변화시키면서 cost를 최소화하는 점을 찾는다.

 

미분 계산 사이트

     미분 계산은 위의 사이트에서 쉽게 할 수 있다고 한다.

convec function

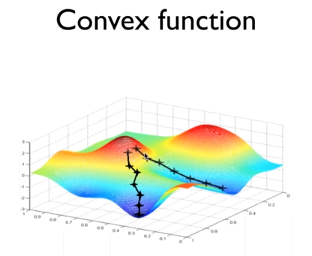
     하지만 한 발짝씩 내려가는 알고리즘에 대해서는 한 번 더 생각해볼 필요가 있다. 위 그림과 같이 시작점에 따라서 최소값에 대한 결과가 다르게 나올 수도 있기 때문이다.

 

      우리의 맨 처음 cost function에서는 위와 같이 convex function이 만들어져서 어느 점에서 시작하더라도 같은 최소값이 되게 된다. 그래서 cost function을 구성할 때 반드시 위와 같은 모양을 이루는지 확인해야 한다.

 

다음 시간에는 multi-variate linear regression을 알아보도록 하겠다.