[DLBasic]Lecture 5-1. Logistic(Regression) Classification

     저번 시간에는 linear regression을 배웠는데 이번 시간에는 Logistic Regression인 Classification을 배우도록 하겠다. 매우 중요한 부분이라고 강조하셨다.

 

Linear Regression 복습

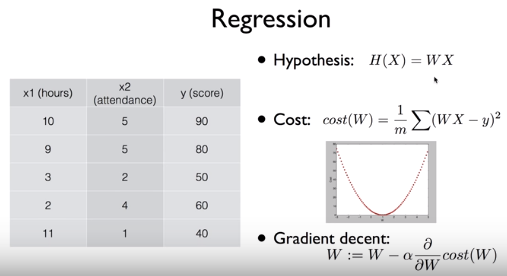
     저번 시간까지 배웠던 Linear Regression을 복습해보자면 위와 같다. Hypothesis, Cost Function, Gradient Descent는 꼭 알아야할 중요한 부분이었다. Hypothesis의 형태가 선형이기 때문에 linear regression이라고 불린 것이었다.

Gradient Descent에서의 alpha 뒤에 나오는 기울기는 Cost function을 미분한 형태이다. 한 번에 얼마나 움직일지가 alpha로 주어진, learning rate라고도 불리는 학습률이다. 이 세 가지만 있으면 linear regression을 이해하고, 구현할 수 있다. classification도 이와 크게 다르지 않다.

 

     Binary Classification은 둘 중의 하나의 카테고리를 고르는 것이다. 그 예로는 spam인지 아닌지, facebook feed를

보일 것인지 숨길 것인지, 신용카드 거래가 적법한지, 사기인지 구분하는 것이 있겠다.

 

기계적으로 encoding

     위의 2가지의 카테고리로 분류하는 것을 컴퓨터에서는 0과 1로 encoding해서 수행한다. 한 쪽 카테고리를 0,

다른 쪽 카테고리는 1로 설정하여 나누는 것이다.

 

악성종양인지 양성 종양인지 분류

이전의 기록을 통해 주식을 사고 팔지 판단

   

Binary classification에 linear regression을 사용해본다면

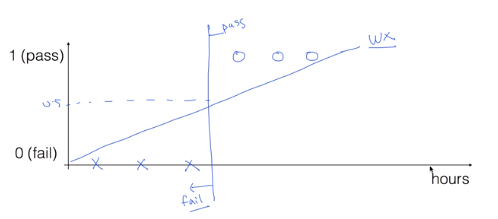
     Binary Classification에 linear regression을 사용한다면 대강 위와 같은 값으로, 0.5 이상은 pass, 0.5 이하는 fail로

생각할 수도 있겠다. 그러나 이 방법에는 문제가 존재한다.

 

새로운 점이 추가되었을 때

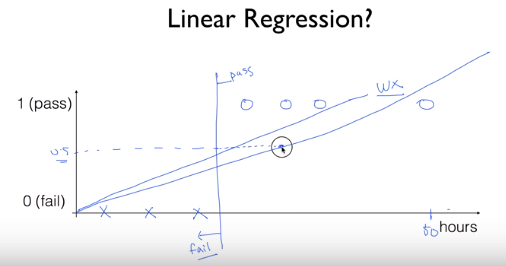
     아까의 그래프에서 만약 새로운 데이터가 추가된다면 그 데이터를 따라서 직선이 기울어지게 되고 그렇다면 0.5

이상이 pass라는 기준이 맞지 않게 된다.

 

classification에 linear regression을 적용했을 때의 또다른 문제

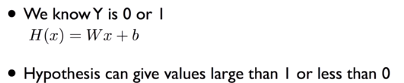
      또 다른 문제로는 binary classification은 결과가 0 아니면 1로 나와야하는데 linear regression은 그 이외의 값이

나올 수도 있다는 점이다. 0보다 훨씬 작거나 1보다 훨씬 큰 값이 나온다면 어떻게 판단해야할지 곤란해진다.

 

     그러므로 linear regression의 H(x) = Wx + b의 결과가 0 또는 1의 값이 나올 수 있게 바꿔주는 g(x)라는 함수를

정의하기로 한다.

Sigmoid Function

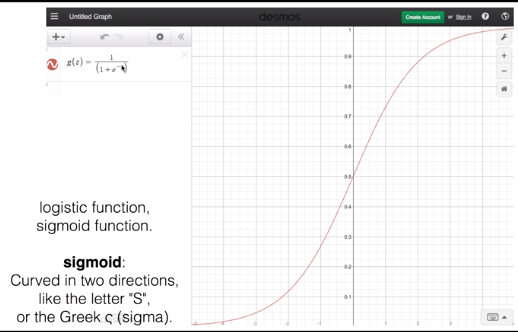
     그래서 찾은 위의 Sigmoid 함수는 0~1 사이의 값이 나오므로 우리의 목적에 적합하다고 할 수 있다.

S 모양이라서 Sigmoid 함수라고 불리고 또는 logistic function이라고 불린다. x가 무한으로 커지면 g 함수의 값은 1에

가까워지고, x가 무한으로 작아지면 g 함수는 0에 가까이 간다.

 

Sigmoid function

     W^TX 부분은 그 형태에 따라 WX로 쓸 수도 있다고 한다.

 

다음 시간에는 logistic regression의 cost function과 그를 최소화하기 위한 방법을 알아보겠다.