[DLBasic] 5-2. Classification : cost function & gradient decent

     저번 시간에는 linear regression과 다소 차이가 있는 logistic regression을 알아봤다. 이번 시간에는 그

logistic regression의 cost function과 그를 최소화하는 법을 알아볼 것이다.

 

linear regression과 logistic regression의 cost function 차이

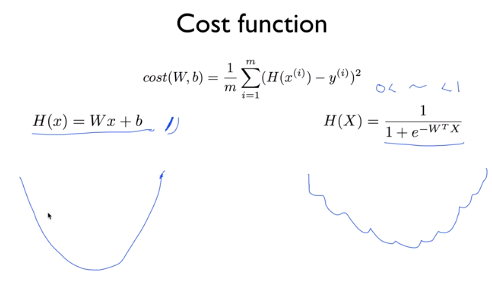
      H(x) = Wx + b의 형태를 사용했던 linear regression과 달리 classification은 sigmoid function을 사용하기

때문에 cost function의 모양도 좀 달라지게 된다. sigmoid function의 값은 0과 1 사이이기 때문에 위와 같이

함수의 모양이 좀 달라진다. 더이상 linear하지 않아져서 시작점이 어디인지에 따라 최소값이 달라질 수 있는

문제가 생긴다.

전체의 최소값, 즉 global minimum을 찾는 것이 우리의 목표인데 한 부분에서는 local minimum을 구해질 수도

있어서 gradient descent algorithm에서는 위와 같은 cost function을 쓸 수 없다.

 

logistic regression에 사용되는 cost function

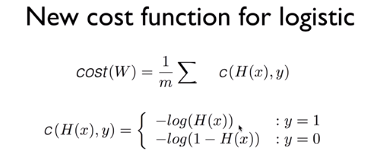
      위에서 언급했던 문제를 해결하기 위해서 logistic regression에서는 위와 같은 새로운 cost function을 쓸 것이다.

위에서 울퉁불퉁한 모양을 만들었던 exponential을 log 함수가 보완한다는 개념이라고 한다.

왼쪽이 y = 1, 오른쪽이 y = 0일때의 cost function

     왼쪽은 y =1 일 때 cost function, 즉 -log(H(x))의 그래프이고, 오른쪽은 y = 0일 때의 cost function,

즉 -log(1-H(x))의 그래프이다. y = 1일 때 만약 예측값이 1이었다면 결과는 0이 되어 cost function이 최소가 되지만,

예측값이 0이었다면 cost function의 결과값은 거의 무한대가 된다.

오른쪽의 경우도 비슷하게 구할 수 있다. 만약 예측값이 0이면 cost function의 결과가 0, 1이면 cost function의 결과가 무한대에 가까워진다. 값이 틀리면 cost function값이 커져서 penalty를 준다는 우리의 목적과 일치한다.

cost function을 하나의 식으로 합치기

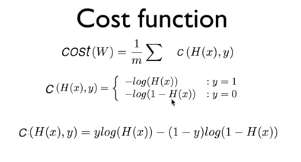
     맨 아래의 cost function앞에 -가 있는데 오타로 나오지 않았다고 한다.

즉, C( H(x), y ) = -ylog(H(x)) - (1 - y)log(1 - H(x))이다.

 

     이제 위의 cost function을 사용하여 최소값을 구하는 gradient descent algorithm을 구해보도록 하겠다.

   

logistic regression의 gradient descent algorithm

     linear regression의 경우와 같이 cost function을 미분하고 학습률을 곱한 값을 뺀다. 

직접 프로그래밍

     minimize할 때는 GradientDescentOptimizer이라는 라이브러리가 이미 있기 때문에 참고하라고 한다.

 

다음 시간에는 Multinomial classifiaction인 softmax regression을 배우도록 하겠다.