[DLBasic] Lecture 4. Multi-variable Linear Regression

     저번 시간에 hypothesis, cost function, gradient descent algorithm에 대해 배웠다.

One input Linear Regression

     또 input이 하나일 때는 위와 같은 data가 나오고 x 하나로 y 하나를 예측하면 된다.

 

 

오늘 배울 것은 여러 개의 input으로 결과 하나를 예측하는 multi-variable linear regression이다.

multi-variable linear regression data

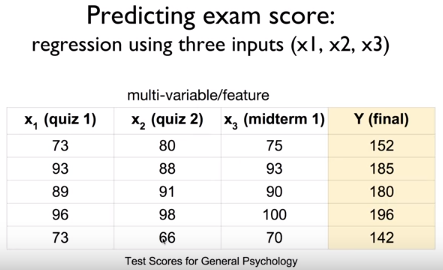
     위와 같은 경우에는 input이 3개이다. 이런 경우에는 변수가 3개나 있어서 이전의 방법과는 다른 방법을 써야한다.

 

input이 3개일 때의 가설과 cost function

     입력이 3개일 때 가설과 cost function은 위와 같은 모양이 될 것이다.

Multi-variable linear regression's Hypothesis

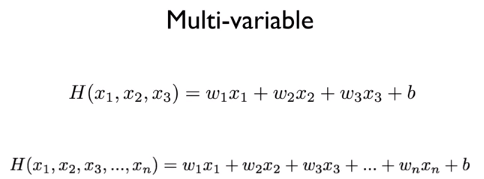
     variable이 더 많은 경우도 위와 같이 설정할 수 있다. 그런데 이렇게 나열하다보니 매우 불편해진다.

그래서 matrix를 사용하려고 한다.

Hypothesis using matrix

    위와 같이 우리의 Hypothesis를 행렬로 표현했다. 간단하게 행렬의 곱셈을 수행하면 원하는 식을 구할 수 있다.

보통 행렬을 쓸 때는 대문자로 표현하고, x를 앞에 쓴다. 

Test Scores for General Psychology

     이 점수 한 줄 한 줄을 instance라고 부른다. 많은 instance가 있을 때에는 위처럼 X 행렬 하나당 W 행렬을 곱할 수도 있지만, 횟수가 너무 많아지므로 아래의 방법을 사용한다.

instance의 수대로 만든 행렬

     위와 같이 instance의 수만큼 행렬을 만드면 한꺼번에 곱해서 결과를 얻을 수 있다.

만약 None이나 -1이 행렬의 행이나 열의 개수로 나타난다면 n개라는 뜻이다.

n output matrix

출력이 꼭 하나일 필요는 없으므로 여러 개의 출력을 확인할 수도 있겠다. 위의 경우에는 [3, 2]의 W를 사용했을 것이다.

matrix를 사용하면 multi-variable일 경우에도, 출력이 여러 개일 때에도 처리할 수 있어서 매우 편리하겠다.

 

다음 시간에는 Logistic Regression인 Classification을 배울 것이다.